Diffusion Models
Diffusion-based neural networks have gained traction in recent years for tasks such as generative AI. In this project, I implement a diffusion-based network for image generation using CIFAR10 dataset. 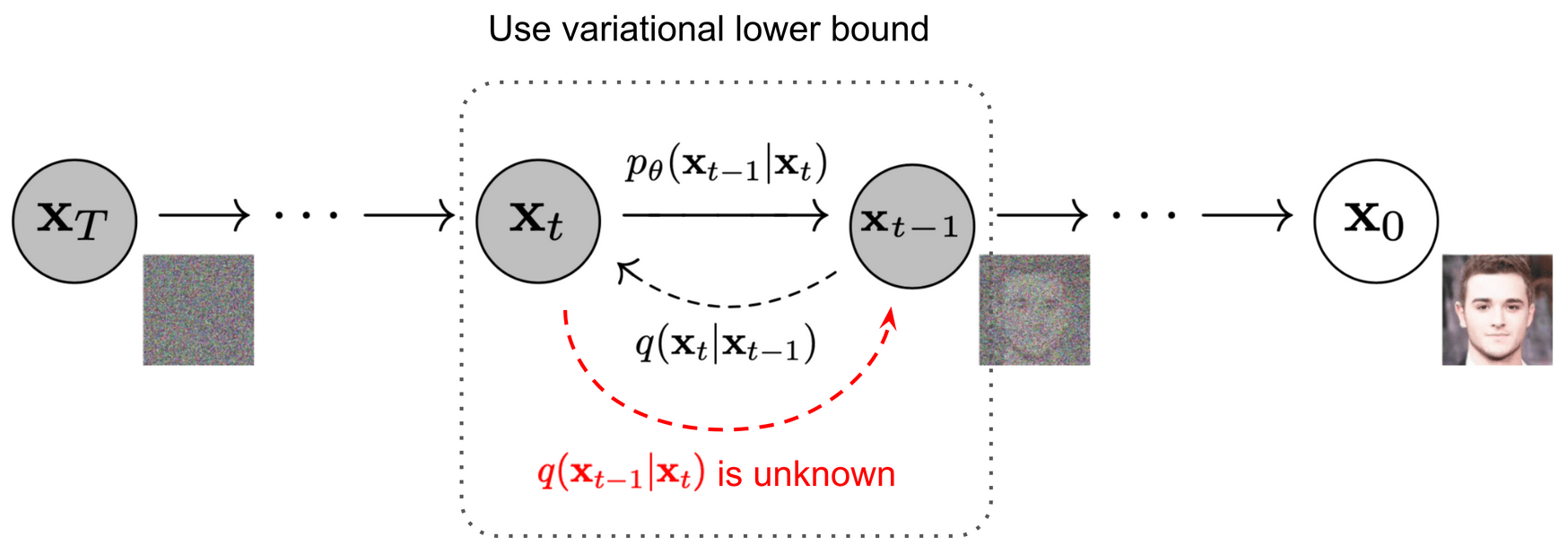
Diffusion model
# Imports
from contextlib import contextmanager
from copy import deepcopy
from glob import glob
import math, os, random
from matplotlib.pyplot import imread # alternative to scipy.misc.imread
import matplotlib.patches as patches
import os.path
from os.path import *
from IPython import display
from matplotlib import pyplot as plt
import torch
from torch import optim, nn, Tensor
from torch.nn import functional as F
from torch.utils import data
from torchvision import datasets, transforms, utils
from torchvision.transforms import functional as TF
from tqdm.notebook import tqdm, trange
# Utilities
@contextmanager
def train_mode(model, mode=True):
"""A context manager that places a model into training mode and restores
the previous mode on exit."""
modes = [module.training for module in model.modules()]
try:
yield model.train(mode)
finally:
for i, module in enumerate(model.modules()):
module.training = modes[i]
def eval_mode(model):
"""A context manager that places a model into evaluation mode and restores
the previous mode on exit."""
return train_mode(model, False)
@torch.no_grad()
def ema_update(model, averaged_model, decay):
"""Incorporates updated model parameters into an exponential moving averaged
version of a model. It should be called after each optimizer step."""
model_params = dict(model.named_parameters())
averaged_params = dict(averaged_model.named_parameters())
assert model_params.keys() == averaged_params.keys()
for name, param in model_params.items():
averaged_params[name].mul_(decay).add_(param, alpha=1 - decay)
model_buffers = dict(model.named_buffers())
averaged_buffers = dict(averaged_model.named_buffers())
assert model_buffers.keys() == averaged_buffers.keys()
for name, buf in model_buffers.items():
averaged_buffers[name].copy_(buf)
class SelfAttention(nn.Module):
def __init__(self, dim_in: int, dim_q: int, dim_v: int):
super().__init__()
"""
This class is used for calculating single head attention.
You will first initialize the layers, then implement
(QK^T / sqrt(d_k))V in function scaled_dot_product.
Finally you'll need to put them all together into the forward funciton.
args:
dim_in: an int value for input sequence embedding dimension
dim_q: an int value for output dimension of query and ley vector
dim_v: an int value for output dimension for value vectors
"""
self.q = None # initialize for query
self.k = None # initialize for key
self.v = None # initialize for value
##########################################################################
# TODO: This function initializes three linear layers to get Q, K, V. #
# Please use the same names for query, key and value transformations #
# as given above. self.q, self.k, and self.v respectively. #
##########################################################################
# Replace "pass" statement with your code
self.q = nn.Linear(dim_in,dim_q)
self.k = nn.Linear(dim_in,dim_q)
self.v = nn.Linear(dim_in,dim_v)
##########################################################################
# END OF YOUR CODE #
##########################################################################
def scaled_dot_product(self,
query: Tensor, key: Tensor, value: Tensor
) -> Tensor:
"""
The function performs a fundamental block for attention mechanism, the scaled
dot product.
args:
query: a Tensor of shape (N,K, M) where N is the batch size, K is the
sequence length and M is the sequence embeding dimension
key: a Tensor of shape (N, K, M) where N is the batch size, K is the
sequence length and M is the sequence embeding dimension
value: a Tensor of shape (N, K, M) where N is the batch size, K is the
sequence length and M is the sequence embeding dimension
return:
y: a tensor of shape (N, K, M) that contains the weighted sum of values
"""
y = None
###############################################################################
# TODO: This function calculates (QK^T / sqrt(d_k))V on a batch scale. #
# Implement this function using no loops. #
###############################################################################
# Replace "pass" statement with your code
# NKM times NMK
output = torch.bmm(query,key.permute(0,2,1)) / math.sqrt(query.shape[2])
output = torch.softmax(output, dim=-1)
y = torch.bmm(output,value)
##############################################################################
# END OF YOUR CODE #
##############################################################################
return y
def forward(
self, query: Tensor, key: Tensor, value: Tensor
) -> Tensor:
"""
An implementation of the forward pass of the self-attention layer.
args:
query: Tensor of shape (N, K, M)
key: Tensor of shape (N, K, M)
value: Tensor of shape (N, K, M)
return:
y: Tensor of shape (N, K, dim_v)
"""
y = None
##########################################################################
# TODO: Implement the forward pass of attention layer with functions #
# defined above. #
##########################################################################
# Replace "pass" statement with your code
y = self.scaled_dot_product(self.q(query),self.k(key),self.v(value))
##########################################################################
# END OF YOUR CODE #
##########################################################################
return y
class MultiHeadAttention(nn.Module):
def __init__(self, num_heads: int, dim_in: int, dim_out: int, dropout_rate:float = 0.1):
super().__init__()
"""
A naive implementation of the MultiheadAttention layer. You will apply
the self attention defined above and concat them together to calculate
multi-head attention.
args:
num_heads: int value specifying the number of heads
dim_in: int value specifying the input dimension of the query, key
and value. This will be the input dimension to each of the
SingleHeadAttention blocks
dim_out: int value specifying the output dimension of the complete
MultiHeadAttention block
"""
##########################################################################
# TODO: Initialize two things here: #
# 1.) Use nn.ModuleList to initialze a list of SingleHeadAttention layer #
# modules.The length of this list should be equal to num_heads with each #
# SingleHeadAttention layer having input dimension as dim_in, and the #
# last dimension of concated heads should be d_out #
# 2.) Use nn.Linear to map the output of nn.Modulelist block back to #
# dim_in. #
##########################################################################
# Replace "pass" statement with your code
self.linearMap = nn.Linear(dim_out,dim_in)
self.attentionList = nn.ModuleList([SelfAttention(dim_in=dim_in, dim_q= dim_out // num_heads, dim_v= dim_out // num_heads) for i in range(num_heads)])
##########################################################################
# END OF YOUR CODE #
##########################################################################
self.dropout = nn.Dropout(dropout_rate)
self.norm = nn.LayerNorm(dim_out)
def forward(
self, x: Tensor
) -> Tensor:
"""
An implementation of the forward pass of the MultiHeadAttention layer.
args:
query: Tensor of shape (N, K, M) where N is the number of sequences in
the batch, K is the sequence length and M is the input embedding
dimension. M should be equal to dim_in in the init function
key: Tensor of shape (N, K, M) where N is the number of sequences in
the batch, K is the sequence length and M is the input embedding
dimension. M should be equal to dim_in in the init function
value: Tensor of shape (N, K, M) where N is the number of sequences in
the batch, K is the sequence length and M is the input embedding
dimension. M should be equal to dim_in in the init function
returns:
y: Tensor of shape (N, K, M)
"""
y = None
n, c, h, w = x.shape
x = x.reshape(n, c, h*w).transpose(-2, -1)
query, key, value = x, x, x
##########################################################################
# TODO: Implement the forward pass of multi-head attention layer with #
# functions defined above. #
##########################################################################
# Replace "pass" statement with your code
heads = torch.zeros((0,0,0),device='cuda')
count = 1
for layer in self.attentionList:
if count==1:
heads = layer(query,key,value)
else:
temp = layer(query,key,value) # (N, K, dim_v)
heads = torch.cat((heads, temp), dim=-1)
count = count + 1
y = self.linearMap(heads)
##########################################################################
# END OF YOUR CODE #
##########################################################################
# Residual connection, normalization and dropout
return self.dropout(self.norm(x) + y).transpose(-2, -1).reshape(n, c, h, w)
# Define the model (a residual U-Net)
class ResidualBlock(nn.Module):
def __init__(self, main, skip=None):
super().__init__()
self.main = nn.Sequential(*main)
self.skip = skip if skip else nn.Identity()
def forward(self, input):
return self.main(input) + self.skip(input)
class ResConvBlock(ResidualBlock):
def __init__(self, c_in, c_mid, c_out, is_last=False):
skip = None if c_in == c_out else nn.Conv2d(c_in, c_out, 1, bias=False)
super().__init__([
nn.Conv2d(c_in, c_mid, 3, padding=1),
nn.Dropout2d(0.1, inplace=True),
nn.ReLU(inplace=True),
nn.Conv2d(c_mid, c_out, 3, padding=1),
nn.Dropout2d(0.1, inplace=True) if not is_last else nn.Identity(),
nn.ReLU(inplace=True) if not is_last else nn.Identity(),
], skip)
class SkipBlock(nn.Module):
def __init__(self, main, skip=None):
super().__init__()
self.main = nn.Sequential(*main)
self.skip = skip if skip else nn.Identity()
def forward(self, input):
return torch.cat([self.main(input), self.skip(input)], dim=1)
class FourierFeatures(nn.Module):
def __init__(self, in_features, out_features, std=1.):
super().__init__()
assert out_features % 2 == 0
self.weight = nn.Parameter(torch.randn([out_features // 2, in_features]) * std)
def forward(self, input):
f = 2 * math.pi * input @ self.weight.T
return torch.cat([f.cos(), f.sin()], dim=-1)
def expand_to_planes(input, shape):
return input[..., None, None].repeat([1, 1, shape[2], shape[3]])
class Diffusion(nn.Module):
def __init__(self):
super().__init__()
c = 64 # The base channel count
self.timestep_embed = FourierFeatures(1, 16)
self.class_embed = nn.Embedding(11, 4)
self.net = nn.Sequential( # 32x32
ResConvBlock(3 + 16 + 4, c, c),
ResConvBlock(c, c, c),
SkipBlock([
nn.AvgPool2d(2), # 32x32 -> 16x16
ResConvBlock(c, c * 2, c * 2),
ResConvBlock(c * 2, c * 2, c * 2),
SkipBlock([
nn.AvgPool2d(2), # 16x16 -> 8x8
ResConvBlock(c * 2, c * 4, c * 4),
MultiHeadAttention(c * 4 // 64, c * 4, c * 4),
ResConvBlock(c * 4, c * 4, c * 4),
MultiHeadAttention(c * 4 // 64, c * 4, c * 4),
SkipBlock([
nn.AvgPool2d(2), # 8x8 -> 4x4
ResConvBlock(c * 4, c * 8, c * 8),
MultiHeadAttention(c * 8 // 64, c * 8, c * 8),
ResConvBlock(c * 8, c * 8, c * 8),
MultiHeadAttention(c * 8 // 64, c * 8, c * 8),
ResConvBlock(c * 8, c * 8, c * 8),
MultiHeadAttention(c * 8 // 64, c * 8, c * 8),
ResConvBlock(c * 8, c * 8, c * 4),
MultiHeadAttention(c * 4 // 64, c * 4, c * 4),
nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False),
]), # 4x4 -> 8x8
ResConvBlock(c * 8, c * 4, c * 4),
MultiHeadAttention(c * 4 // 64, c * 4, c * 4),
ResConvBlock(c * 4, c * 4, c * 2),
MultiHeadAttention(c * 2 // 64, c * 2, c * 2),
nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False),
]), # 8x8 -> 16x16
ResConvBlock(c * 4, c * 2, c * 2),
ResConvBlock(c * 2, c * 2, c),
nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False),
]), # 16x16 -> 32x32
ResConvBlock(c * 2, c, c),
ResConvBlock(c, c, 3, is_last=True),
)
def forward(self, input, t, cond):
timestep_embed = expand_to_planes(self.timestep_embed(t[:, None]), input.shape)
class_embed = expand_to_planes(self.class_embed(cond + 1), input.shape)
return self.net(torch.cat([input, class_embed, timestep_embed], dim=1))
TODO: (b) implement sampling process of diffusion model
In this problem, you will perform classifier-free guidance for sampling.
# Define the noise schedule and sampling loop
def get_alphas_sigmas(t):
"""Returns the scaling factors for the clean image (alpha) and for the
noise (sigma), given a timestep."""
return torch.cos(t * math.pi / 2), torch.sin(t * math.pi / 2)
@torch.no_grad()
def sample(model, x, steps, eta, classes, guidance_scale=1.):
"""Draws samples from a model given starting noise."""
ts = x.new_ones([x.shape[0]])
# Create the noise schedule
t = torch.linspace(1, 0, steps + 1)[:-1]
alphas, sigmas = get_alphas_sigmas(t)
# The sampling loop
for i in trange(steps):
# Get the model output (v, the predicted velocity)
##########################################################################
# TODO: Perform classifier-free guidance:
# 1.) Generate inputs for both conditional images and unconditional #
# images given their class. #
# Hint: To generate unconditional input, copy the input images and time #
# stamps and stack them with the original input images and time stamps. #
# The only thing you need to change is the create the unconditional #
# class "-1" and stack it with the input conditional class. Thus You #
# will have a tensor of twice of the batch size of the original input.
# 2.) Pass your stacked input to the model to get both conditional and #
# unconditional vecocity.
# 3.) Compute v = v_uncond + guidance_scale * (v_cond - v_uncond) #
##########################################################################
# Replace "pass" statement with your code
#print(x.shape)
#print(t.shape)
#print(classes.shape)
z = torch.cat((x,x), dim=0).cuda()
z_class = torch.cat((classes, -1*torch.ones_like(classes)), dim=0).cuda()
z_time = torch.cat((t[i]*torch.ones_like(classes), t[i]*torch.ones_like(classes)), dim=0).cuda()
#print(z.shape)
#print(z_time.shape)
#print(z_class.shape)
output = model(z,z_time,z_class)
v_cond, v_uncond = torch.chunk(output, 2, dim=0)
v = v_uncond + guidance_scale*(v_cond - v_uncond)
##########################################################################
# END OF YOUR CODE #
##########################################################################
# Predict the noise and the denoised image
pred = x * alphas[i] - v * sigmas[i]
eps = x * sigmas[i] + v * alphas[i]
# If we are not on the last timestep, compute the noisy image for the
# next timestep.
if i < steps - 1:
# If eta > 0, adjust the scaling factor for the predicted noise
# downward according to the amount of additional noise to add
ddim_sigma = eta * (sigmas[i + 1]**2 / sigmas[i]**2).sqrt() * \
(1 - alphas[i]**2 / alphas[i + 1]**2).sqrt()
adjusted_sigma = (sigmas[i + 1]**2 - ddim_sigma**2).sqrt()
# Recombine the predicted noise and predicted denoised image in the
# correct proportions for the next step
x = pred * alphas[i + 1] + eps * adjusted_sigma
# Add the correct amount of fresh noise
if eta:
x += torch.randn_like(x) * ddim_sigma
# If we are on the last timestep, output the denoised image
return pred
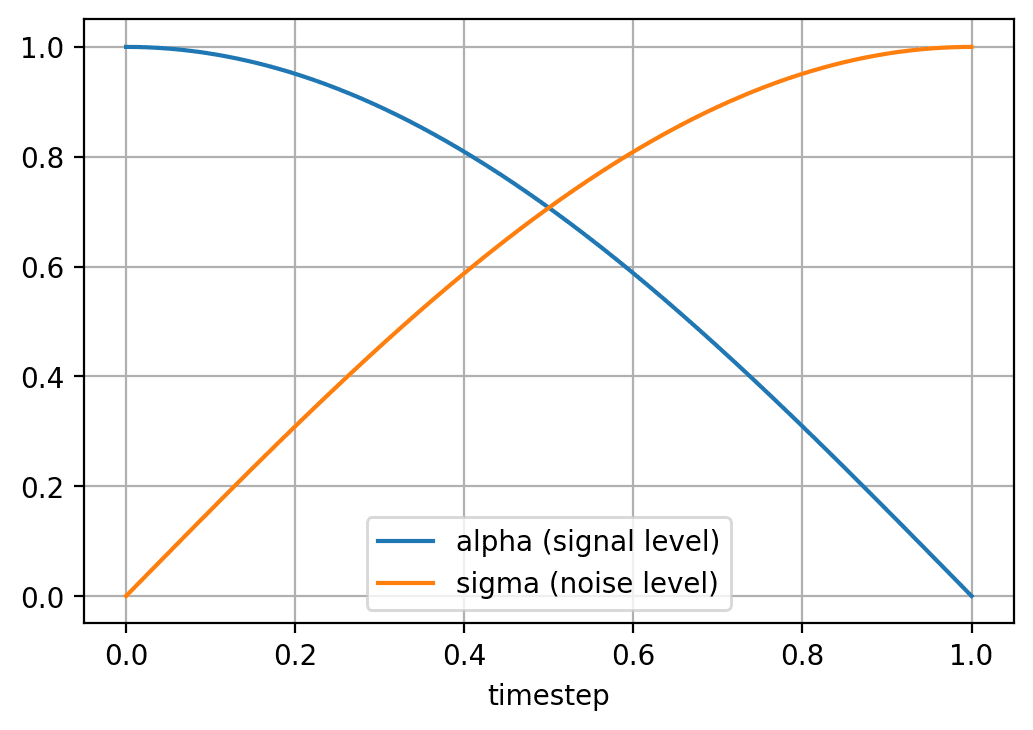
# Visualize the noise schedule
%config InlineBackend.figure_format = 'retina'
plt.rcParams['figure.dpi'] = 100
t_vis = torch.linspace(0, 1, 1000)
alphas_vis, sigmas_vis = get_alphas_sigmas(t_vis)
print('The noise schedule:')
plt.plot(t_vis, alphas_vis, label='alpha (signal level)')
plt.plot(t_vis, sigmas_vis, label='sigma (noise level)')
plt.legend()
plt.xlabel('timestep')
plt.grid()
plt.show()
The noise schedule:
# Prepare the dataset
batch_size = 100
tf = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5]),
])
train_set = datasets.CIFAR10('data', train=True, download=True, transform=tf)
train_dl = data.DataLoader(train_set, batch_size, shuffle=True,
num_workers=1, persistent_workers=True, pin_memory=True)
val_set = datasets.CIFAR10('data', train=False, download=True, transform=tf)
val_dl = data.DataLoader(val_set, batch_size,
num_workers=1, persistent_workers=True, pin_memory=True)
Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to data/cifar-10-python.tar.gz
0%| | 0/170498071 [00:00<?, ?it/s]
Extracting data/cifar-10-python.tar.gz to data
Files already downloaded and verified
# Create the model and optimizer
seed = 0
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print('Using device:', device)
torch.manual_seed(0)
model = Diffusion().to(device)
model_ema = deepcopy(model)
print('Model parameters:', sum(p.numel() for p in model.parameters()))
opt = optim.Adam(model.parameters(), lr=2e-4)
scaler = torch.cuda.amp.GradScaler()
epoch = 0
# Use a low discrepancy quasi-random sequence to sample uniformly distributed
# timesteps. This considerably reduces the between-batch variance of the loss.
rng = torch.quasirandom.SobolEngine(1, scramble=True)
Using device: cuda
Model parameters: 27487287
As a sanity check, the total number of parameters in your model should match the following.
Model parameters: 27487287
# Actually train the model
ema_decay = 0.999
# The number of timesteps to use when sampling
steps = 500
# The amount of noise to add each timestep when sampling
# 0 = no noise (DDIM)
# 1 = full noise (DDPM)
eta = 1.
# Classifier-free guidance scale (0 is unconditional, 1 is conditional)
guidance_scale = 2.
def eval_loss(model, rng, reals, classes):
# Draw uniformly distributed continuous timesteps
t = rng.draw(reals.shape[0])[:, 0].to(device)
# Calculate the noise schedule parameters for those timesteps
alphas, sigmas = get_alphas_sigmas(t)
# Combine the ground truth images and the noise
alphas = alphas[:, None, None, None]
sigmas = sigmas[:, None, None, None]
noise = torch.randn_like(reals)
noised_reals = reals * alphas + noise * sigmas
targets = noise * alphas - reals * sigmas
# Drop out the class on 20% of the examples
to_drop = torch.rand(classes.shape, device=classes.device).le(0.2)
classes_drop = torch.where(to_drop, -torch.ones_like(classes), classes)
# Compute the model output and the loss.
#print(noised_reals.shape)
#print(t.shape)
#print(classes_drop.shape)
v = model(noised_reals, t, classes_drop)
return F.mse_loss(v, targets)
def train():
for i, (reals, classes) in enumerate(tqdm(train_dl)):
opt.zero_grad()
reals = reals.to(device)
classes = classes.to(device)
# Evaluate the loss
loss = eval_loss(model, rng, reals, classes)
# Do the optimizer step and EMA update
scaler.scale(loss).backward()
scaler.step(opt)
ema_update(model, model_ema, 0.95 if epoch < 5 else ema_decay)
scaler.update()
if i % 50 == 0:
tqdm.write(f'Epoch: {epoch}, iteration: {i}, loss: {loss.item():g}')
@torch.no_grad()
@torch.random.fork_rng()
@eval_mode(model_ema)
def val():
tqdm.write('\nValidating...')
torch.manual_seed(seed)
rng = torch.quasirandom.SobolEngine(1, scramble=True)
total_loss = 0
count = 0
for i, (reals, classes) in enumerate(tqdm(val_dl)):
reals = reals.to(device)
classes = classes.to(device)
loss = eval_loss(model_ema, rng, reals, classes)
total_loss += loss.item() * len(reals)
count += len(reals)
loss = total_loss / count
tqdm.write(f'Validation: Epoch: {epoch}, loss: {loss:g}')
@torch.no_grad()
@torch.random.fork_rng()
@eval_mode(model_ema)
def demo():
tqdm.write('\nSampling...')
torch.manual_seed(seed)
noise = torch.randn([100, 3, 32, 32], device=device)
fakes_classes = torch.arange(10, device=device).repeat_interleave(10, 0)
fakes = sample(model_ema, noise, steps, eta, fakes_classes, guidance_scale)
grid = utils.make_grid(fakes, 10).cpu()
filename = f'demo_{epoch:05}.png'
TF.to_pil_image(grid.add(1).div(2).clamp(0, 1)).save(filename)
display.display(display.Image(filename))
tqdm.write('')
# Each epoch might take up to 2.5 minutes
print("Initial noise")
val()
demo()
while epoch <= 20:
print('Epoch', epoch)
train()
if epoch % 5 == 0:
val()
demo()
epoch += 1
Initial noise
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 0, loss: 0.659573
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 0
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 0, iteration: 0, loss: 0.651582
Epoch: 0, iteration: 50, loss: 0.332843
Epoch: 0, iteration: 100, loss: 0.217117
Epoch: 0, iteration: 150, loss: 0.199165
Epoch: 0, iteration: 200, loss: 0.194742
Epoch: 0, iteration: 250, loss: 0.182038
Epoch: 0, iteration: 300, loss: 0.18094
Epoch: 0, iteration: 350, loss: 0.18694
Epoch: 0, iteration: 400, loss: 0.176955
Epoch: 0, iteration: 450, loss: 0.177187
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 0, loss: 0.156553
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 1
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 1, iteration: 0, loss: 0.161872
Epoch: 1, iteration: 50, loss: 0.171297
Epoch: 1, iteration: 100, loss: 0.160897
Epoch: 1, iteration: 150, loss: 0.165521
Epoch: 1, iteration: 200, loss: 0.170159
Epoch: 1, iteration: 250, loss: 0.156866
Epoch: 1, iteration: 300, loss: 0.158521
Epoch: 1, iteration: 350, loss: 0.146488
Epoch: 1, iteration: 400, loss: 0.153386
Epoch: 1, iteration: 450, loss: 0.155603
Epoch 2
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 2, iteration: 0, loss: 0.140036
Epoch: 2, iteration: 50, loss: 0.155009
Epoch: 2, iteration: 100, loss: 0.156991
Epoch: 2, iteration: 150, loss: 0.1518
Epoch: 2, iteration: 200, loss: 0.145272
Epoch: 2, iteration: 250, loss: 0.150071
Epoch: 2, iteration: 300, loss: 0.135371
Epoch: 2, iteration: 350, loss: 0.153224
Epoch: 2, iteration: 400, loss: 0.144792
Epoch: 2, iteration: 450, loss: 0.145422
Epoch 3
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 3, iteration: 0, loss: 0.144276
Epoch: 3, iteration: 50, loss: 0.150701
Epoch: 3, iteration: 100, loss: 0.137814
Epoch: 3, iteration: 150, loss: 0.135317
Epoch: 3, iteration: 200, loss: 0.130542
Epoch: 3, iteration: 250, loss: 0.140396
Epoch: 3, iteration: 300, loss: 0.135144
Epoch: 3, iteration: 350, loss: 0.15488
Epoch: 3, iteration: 400, loss: 0.141263
Epoch: 3, iteration: 450, loss: 0.148619
Epoch 4
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 4, iteration: 0, loss: 0.137663
Epoch: 4, iteration: 50, loss: 0.13301
Epoch: 4, iteration: 100, loss: 0.141802
Epoch: 4, iteration: 150, loss: 0.144013
Epoch: 4, iteration: 200, loss: 0.136633
Epoch: 4, iteration: 250, loss: 0.141837
Epoch: 4, iteration: 300, loss: 0.155173
Epoch: 4, iteration: 350, loss: 0.140223
Epoch: 4, iteration: 400, loss: 0.139733
Epoch: 4, iteration: 450, loss: 0.125754
Epoch 5
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 5, iteration: 0, loss: 0.131556
Epoch: 5, iteration: 50, loss: 0.131902
Epoch: 5, iteration: 100, loss: 0.129277
Epoch: 5, iteration: 150, loss: 0.148592
Epoch: 5, iteration: 200, loss: 0.143967
Epoch: 5, iteration: 250, loss: 0.136355
Epoch: 5, iteration: 300, loss: 0.124331
Epoch: 5, iteration: 350, loss: 0.136628
Epoch: 5, iteration: 400, loss: 0.134302
Epoch: 5, iteration: 450, loss: 0.145535
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 5, loss: 0.12703
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 6
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 6, iteration: 0, loss: 0.134856
Epoch: 6, iteration: 50, loss: 0.135705
Epoch: 6, iteration: 100, loss: 0.131178
Epoch: 6, iteration: 150, loss: 0.140955
Epoch: 6, iteration: 200, loss: 0.118933
Epoch: 6, iteration: 250, loss: 0.124761
Epoch: 6, iteration: 300, loss: 0.120303
Epoch: 6, iteration: 350, loss: 0.131072
Epoch: 6, iteration: 400, loss: 0.143108
Epoch: 6, iteration: 450, loss: 0.128755
Epoch 7
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 7, iteration: 0, loss: 0.143316
Epoch: 7, iteration: 50, loss: 0.146673
Epoch: 7, iteration: 100, loss: 0.136365
Epoch: 7, iteration: 150, loss: 0.127349
Epoch: 7, iteration: 200, loss: 0.132875
Epoch: 7, iteration: 250, loss: 0.127841
Epoch: 7, iteration: 300, loss: 0.132054
Epoch: 7, iteration: 350, loss: 0.131102
Epoch: 7, iteration: 400, loss: 0.135398
Epoch: 7, iteration: 450, loss: 0.141991
Epoch 8
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 8, iteration: 0, loss: 0.127125
Epoch: 8, iteration: 50, loss: 0.130177
Epoch: 8, iteration: 100, loss: 0.121372
Epoch: 8, iteration: 150, loss: 0.12809
Epoch: 8, iteration: 200, loss: 0.122419
Epoch: 8, iteration: 250, loss: 0.13347
Epoch: 8, iteration: 300, loss: 0.127105
Epoch: 8, iteration: 350, loss: 0.143767
Epoch: 8, iteration: 400, loss: 0.130068
Epoch: 8, iteration: 450, loss: 0.130407
Epoch 9
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 9, iteration: 0, loss: 0.122439
Epoch: 9, iteration: 50, loss: 0.134249
Epoch: 9, iteration: 100, loss: 0.126405
Epoch: 9, iteration: 150, loss: 0.143927
Epoch: 9, iteration: 200, loss: 0.127004
Epoch: 9, iteration: 250, loss: 0.141481
Epoch: 9, iteration: 300, loss: 0.130491
Epoch: 9, iteration: 350, loss: 0.113528
Epoch: 9, iteration: 400, loss: 0.12173
Epoch: 9, iteration: 450, loss: 0.136158
Epoch 10
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 10, iteration: 0, loss: 0.120233
Epoch: 10, iteration: 50, loss: 0.126944
Epoch: 10, iteration: 100, loss: 0.140046
Epoch: 10, iteration: 150, loss: 0.12829
Epoch: 10, iteration: 200, loss: 0.139348
Epoch: 10, iteration: 250, loss: 0.128343
Epoch: 10, iteration: 300, loss: 0.130207
Epoch: 10, iteration: 350, loss: 0.130892
Epoch: 10, iteration: 400, loss: 0.127476
Epoch: 10, iteration: 450, loss: 0.132228
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 10, loss: 0.122567
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 11
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 11, iteration: 0, loss: 0.130918
Epoch: 11, iteration: 50, loss: 0.120101
Epoch: 11, iteration: 100, loss: 0.133638
Epoch: 11, iteration: 150, loss: 0.132251
Epoch: 11, iteration: 200, loss: 0.121675
Epoch: 11, iteration: 250, loss: 0.127211
Epoch: 11, iteration: 300, loss: 0.117109
Epoch: 11, iteration: 350, loss: 0.139316
Epoch: 11, iteration: 400, loss: 0.129785
Epoch: 11, iteration: 450, loss: 0.133046
Epoch 12
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 12, iteration: 0, loss: 0.123713
Epoch: 12, iteration: 50, loss: 0.136635
Epoch: 12, iteration: 100, loss: 0.118676
Epoch: 12, iteration: 150, loss: 0.129554
Epoch: 12, iteration: 200, loss: 0.134306
Epoch: 12, iteration: 250, loss: 0.128326
Epoch: 12, iteration: 300, loss: 0.130398
Epoch: 12, iteration: 350, loss: 0.136631
Epoch: 12, iteration: 400, loss: 0.124065
Epoch: 12, iteration: 450, loss: 0.124857
Epoch 13
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 13, iteration: 0, loss: 0.124613
Epoch: 13, iteration: 50, loss: 0.126895
Epoch: 13, iteration: 100, loss: 0.131537
Epoch: 13, iteration: 150, loss: 0.122238
Epoch: 13, iteration: 200, loss: 0.126169
Epoch: 13, iteration: 250, loss: 0.135098
Epoch: 13, iteration: 300, loss: 0.133218
Epoch: 13, iteration: 350, loss: 0.122649
Epoch: 13, iteration: 400, loss: 0.120709
Epoch: 13, iteration: 450, loss: 0.126857
Epoch 14
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 14, iteration: 0, loss: 0.131384
Epoch: 14, iteration: 50, loss: 0.1297
Epoch: 14, iteration: 100, loss: 0.131168
Epoch: 14, iteration: 150, loss: 0.132369
Epoch: 14, iteration: 200, loss: 0.12907
Epoch: 14, iteration: 250, loss: 0.125245
Epoch: 14, iteration: 300, loss: 0.120541
Epoch: 14, iteration: 350, loss: 0.123597
Epoch: 14, iteration: 400, loss: 0.134166
Epoch: 14, iteration: 450, loss: 0.136715
Epoch 15
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 15, iteration: 0, loss: 0.128904
Epoch: 15, iteration: 50, loss: 0.126215
Epoch: 15, iteration: 100, loss: 0.121267
Epoch: 15, iteration: 150, loss: 0.118806
Epoch: 15, iteration: 200, loss: 0.126374
Epoch: 15, iteration: 250, loss: 0.139649
Epoch: 15, iteration: 300, loss: 0.12294
Epoch: 15, iteration: 350, loss: 0.131118
Epoch: 15, iteration: 400, loss: 0.127799
Epoch: 15, iteration: 450, loss: 0.13431
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 15, loss: 0.119779
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epoch 16
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 16, iteration: 0, loss: 0.125729
Epoch: 16, iteration: 50, loss: 0.118473
Epoch: 16, iteration: 100, loss: 0.126334
Epoch: 16, iteration: 150, loss: 0.130862
Epoch: 16, iteration: 200, loss: 0.127835
Epoch: 16, iteration: 250, loss: 0.126139
Epoch: 16, iteration: 300, loss: 0.133577
Epoch: 16, iteration: 350, loss: 0.127716
Epoch: 16, iteration: 400, loss: 0.124571
Epoch: 16, iteration: 450, loss: 0.128462
Epoch 17
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 17, iteration: 0, loss: 0.133177
Epoch: 17, iteration: 50, loss: 0.122615
Epoch: 17, iteration: 100, loss: 0.128418
Epoch: 17, iteration: 150, loss: 0.126071
Epoch: 17, iteration: 200, loss: 0.137689
Epoch: 17, iteration: 250, loss: 0.12635
Epoch: 17, iteration: 300, loss: 0.124098
Epoch: 17, iteration: 350, loss: 0.11554
Epoch: 17, iteration: 400, loss: 0.12735
Epoch: 17, iteration: 450, loss: 0.132917
Epoch 18
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 18, iteration: 0, loss: 0.118042
Epoch: 18, iteration: 50, loss: 0.130607
Epoch: 18, iteration: 100, loss: 0.130764
Epoch: 18, iteration: 150, loss: 0.141313
Epoch: 18, iteration: 200, loss: 0.115767
Epoch: 18, iteration: 250, loss: 0.117925
Epoch: 18, iteration: 300, loss: 0.118179
Epoch: 18, iteration: 350, loss: 0.127093
Epoch: 18, iteration: 400, loss: 0.12852
Epoch: 18, iteration: 450, loss: 0.138892
Epoch 19
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 19, iteration: 0, loss: 0.134342
Epoch: 19, iteration: 50, loss: 0.126142
Epoch: 19, iteration: 100, loss: 0.11547
Epoch: 19, iteration: 150, loss: 0.112161
Epoch: 19, iteration: 200, loss: 0.129683
Epoch: 19, iteration: 250, loss: 0.122645
Epoch: 19, iteration: 300, loss: 0.131664
Epoch: 19, iteration: 350, loss: 0.134281
Epoch: 19, iteration: 400, loss: 0.125884
Epoch: 19, iteration: 450, loss: 0.131864
Epoch 20
0%| | 0/500 [00:00<?, ?it/s]
Epoch: 20, iteration: 0, loss: 0.126991
Epoch: 20, iteration: 50, loss: 0.117396
Epoch: 20, iteration: 100, loss: 0.124519
Epoch: 20, iteration: 150, loss: 0.124897
Epoch: 20, iteration: 200, loss: 0.131115
Epoch: 20, iteration: 250, loss: 0.12099
Epoch: 20, iteration: 300, loss: 0.134515
Epoch: 20, iteration: 350, loss: 0.118051
Epoch: 20, iteration: 400, loss: 0.123112
Epoch: 20, iteration: 450, loss: 0.121092
Validating...
0%| | 0/100 [00:00<?, ?it/s]
Validation: Epoch: 20, loss: 0.118257
Sampling...
0%| | 0/500 [00:00<?, ?it/s]

Epipolar Geometry
Download the temple stereo images from the Middlebury stereo dataset.
!wget https://vision.middlebury.edu/mview/data/data/templeSparseRing.zip
!unzip templeSparseRing.zip
--2022-12-02 21:19:30-- https://vision.middlebury.edu/mview/data/data/templeSparseRing.zip
Resolving vision.middlebury.edu (vision.middlebury.edu)... 140.233.20.14
Connecting to vision.middlebury.edu (vision.middlebury.edu)|140.233.20.14|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 4004383 (3.8M) [application/zip]
Saving to: ‘templeSparseRing.zip’
templeSparseRing.zi 100%[===================>] 3.82M 5.32MB/s in 0.7s
2022-12-02 21:19:32 (5.32 MB/s) - ‘templeSparseRing.zip’ saved [4004383/4004383]
Archive: templeSparseRing.zip
creating: templeSparseRing/
inflating: templeSparseRing/templeSR_ang.txt
inflating: templeSparseRing/templeSR0001.png
inflating: templeSparseRing/templeSR0002.png
inflating: templeSparseRing/templeSR0003.png
inflating: templeSparseRing/templeSR0004.png
inflating: templeSparseRing/templeSR0005.png
inflating: templeSparseRing/templeSR0006.png
inflating: templeSparseRing/templeSR0007.png
inflating: templeSparseRing/templeSR0008.png
inflating: templeSparseRing/templeSR0009.png
inflating: templeSparseRing/templeSR0010.png
inflating: templeSparseRing/templeSR0011.png
inflating: templeSparseRing/templeSR0012.png
inflating: templeSparseRing/templeSR0013.png
inflating: templeSparseRing/templeSR0014.png
inflating: templeSparseRing/templeSR0015.png
inflating: templeSparseRing/templeSR0016.png
inflating: templeSparseRing/templeSR_par.txt
inflating: templeSparseRing/README.txt
def process_parameters():
"""
Reads the parameters for the Middlebury dataset
:return: an intrinsics matrix containing the camera parameters and
a list of extrinsics matrices representing mapping from the world to camera coordinates
"""
intrinsics = []
extrinsics = []
with open(os.path.join("templeSparseRing", "templeSR_par.txt"), 'r') as f:
_ = f.readline()
for line in f:
raw_data = line.split()
# Read camera parameters K (intrinsics matrix)
camera_params = np.array(raw_data[1:10]).reshape((3, 3)).astype(float)
intrinsics.append(camera_params)
# Read homogeneous transformation (extrinsics matrix)
rotation = np.array(raw_data[10:19]).reshape((3, 3)).astype(float)
translation = np.array(raw_data[19:]).reshape((3, 1)).astype(float)
extrinsics.append(np.hstack([rotation, translation]))
return intrinsics[0], extrinsics
We will select the first image as the reference frame and transform all the extrinsics matrices.
def set_reference(extrinsics):
"""
Set the first image as reference frame such that its transformation
becomes the identity, apply the inverse of the extrinsics matrix of
the reference frame to all other extrinsics matrices
:param extrinsics: list of original extrinsics matrices
:return: list of transformed extrinsics matrices
"""
shifted_extrinsics = []
stacked = np.vstack([extrinsics[0], [0, 0, 0, 1]])
inv_ref = np.linalg.inv(stacked)
for ex in extrinsics:
stacked = np.vstack([ex, [0, 0, 0, 1]])
transformed = np.matmul(stacked, inv_ref)
transformed /= transformed[-1, -1]
shifted_extrinsics.append(transformed[:3, :])
return shifted_extrinsics
TODO: (a) Back-projection
You can use the fundamental matrix to find the epipolar line in another image frame. Alternatively, you can also back-project the pixel in the reference image at different depths. The back-projected pixels will all fall along a ray that resembles the epipolar line.
import numpy as np
def coordinate_transform(intrinsics, extrinsics, pixel, d, i):
"""
Transform image coordiantes from the reference frame to the second image given a depth d
:param intrinsics: the matrix K storing the camera parameters
:param extrinsics: list of 3 x 4 extrinsics matricies [R | t]
:param pixel: tuple of two ints representing x and y coordinates on the reference image
:param d: a float representing a distance
:param i: int at the end of the image name (4 represents templeSR0004.png)
:return: pixel_coord, a tuple of ints representing the x, y coordinates on the second image
"""
extrinsics_img2 = extrinsics[i - 1]
##########################################################################
# TODO: Implement the coordinate transformation #
##########################################################################
# Replace "pass" statement with your code
# Back-project pixel x in reference frame to world coordinates X
# X = K^-1 @ x * d
# Forward project point X to the second image's pixel coordinates x
# pixel_coord = K @ extrinsics_img2 @ X
x,y = pixel[0], pixel[1]
coord = np.array([[x], [y], [1]])
X = np.linalg.inv(intrinsics) @ coord * d
tempCoord = np.array([ [X[0]],[X[1]],[X[2]],[1] ],dtype=object)
projectedCoord = intrinsics @ extrinsics_img2 @ tempCoord
pixel_coord = projectedCoord/projectedCoord[2]
pixel_coord = pixel_coord[0:2]
##########################################################################
# END OF YOUR CODE #
##########################################################################
return pixel_coord.astype(int)
(b) Compute fundamental matrix
def compute_fundamental_matrix(intrinsics, extrinsics, i):
"""
Compute the fundamental matrix between the i-th image frame and the
reference image frame
:param intrinsics: the intrinsics camera matrix
:param extrinsics: list of original extrinsics matrices
:param i: int at the end of the image name (2 represents templeSR0002.png)
:return: list of transformed extrinsics matrices
"""
rot = extrinsics[i - 1][:3, :3]
trans = extrinsics[i - 1][:3, 3]
# Compute the epipole and fundamental matrix
# e = K R^T t
epipole = intrinsics @ rot.T @ trans
epipole_cross = np.array([[0, -epipole[2], epipole[1]], [epipole[2], 0, -epipole[0]], [-epipole[1], epipole[0], 0]])
# F = K'^(-T)RK^T[e]_x
fundamental = np.linalg.inv(intrinsics).T @ rot @ intrinsics.T @ epipole_cross
fundamental /= fundamental[-1, -1]
return fundamental
(c) Visualize epipolar line
You will then visualize the epipolar line with both the fundamental matrix and the back-projected ray.
def visualize_epipolar_line(pixel, intrinsics, extrinsics, fundamental, i):
"""
Visualizes the pixel in the reference frame, and its corresponding
epipolar line in the i-th image frame
:param pixel: a tuple of (x, y) coordinates in the reference image
:param fundamental: fundamental matrix
:param i: int at the end of the image name (4 represents templeSR0004.png)
"""
img1 = imread(os.path.join("templeSparseRing", "templeSR0001.png"))
img2 = imread(sorted(glob(os.path.join("templeSparseRing", "*.png")))[i - 1])
# Plot reference image with a chosen pixel
_, ax = plt.subplots(1, 3, figsize=(img1.shape[1] * 3 / 80, img1.shape[0] / 80))
ax[0].imshow(img1)
ax[0].add_patch(patches.Rectangle(pixel, 5, 5))
ax[0].title.set_text('Reference Frame')
# Compute epipolar_line from fundamental matrix and the pixel coordinates
# Hartley Zisserman page 246: "I' = Fx is the epipolar line corresponding to x"
# Epipolar line l' in image 2's coordinates
epipolar_line = fundamental @ np.array([pixel[0], pixel[1], 1]).T
# Plot epipolar line from fundamental matrix in second image
x = np.arange(img2.shape[1])
y = np.array((-epipolar_line[0] * x - epipolar_line[2]) / epipolar_line[1])
indices = np.where(np.logical_and(y >= 0, y <= img2.shape[0]))
ax[1].imshow(img2)
ax[1].plot(x[indices], y[indices])
ax[1].title.set_text('Epipolar Line from Fundamental Matrix in templeSR000' + str(i))
# Epipolar line from backprojected ray of different depths
ax[2].imshow(img2)
ax[2].title.set_text('Epipolar Line from Backprojected Ray in templeSR000' + str(i))
for d in np.arange(0.4, 0.8, 0.005):
pixel_coord = coordinate_transform(intrinsics, extrinsics, pixel, d, i)
if pixel_coord[0] >= 0 and pixel_coord[1] >= 0 and pixel_coord[0] + 3 < \
img1.shape[1] and pixel_coord[1] + 3:
ax[2].add_patch(patches.Rectangle((pixel_coord[0], pixel_coord[1]), 3, 3))
plt.show()
# TODO: Feel free to try different images and pixel coordinates
# image_frame is the image number (i.e. 4 is templeSR0004.png)
image_frame = 4
# pixel location (x, y) in the reference frame
pixel = (500, 200)
intrinsics, extrinsics = process_parameters()
shifted_extrinsics = set_reference(extrinsics)
fundamental = compute_fundamental_matrix(intrinsics, shifted_extrinsics, i=image_frame)
visualize_epipolar_line(pixel, intrinsics, shifted_extrinsics, fundamental, i=image_frame)

