Smooth optimization algorithms for global and locally low-rank regularizers

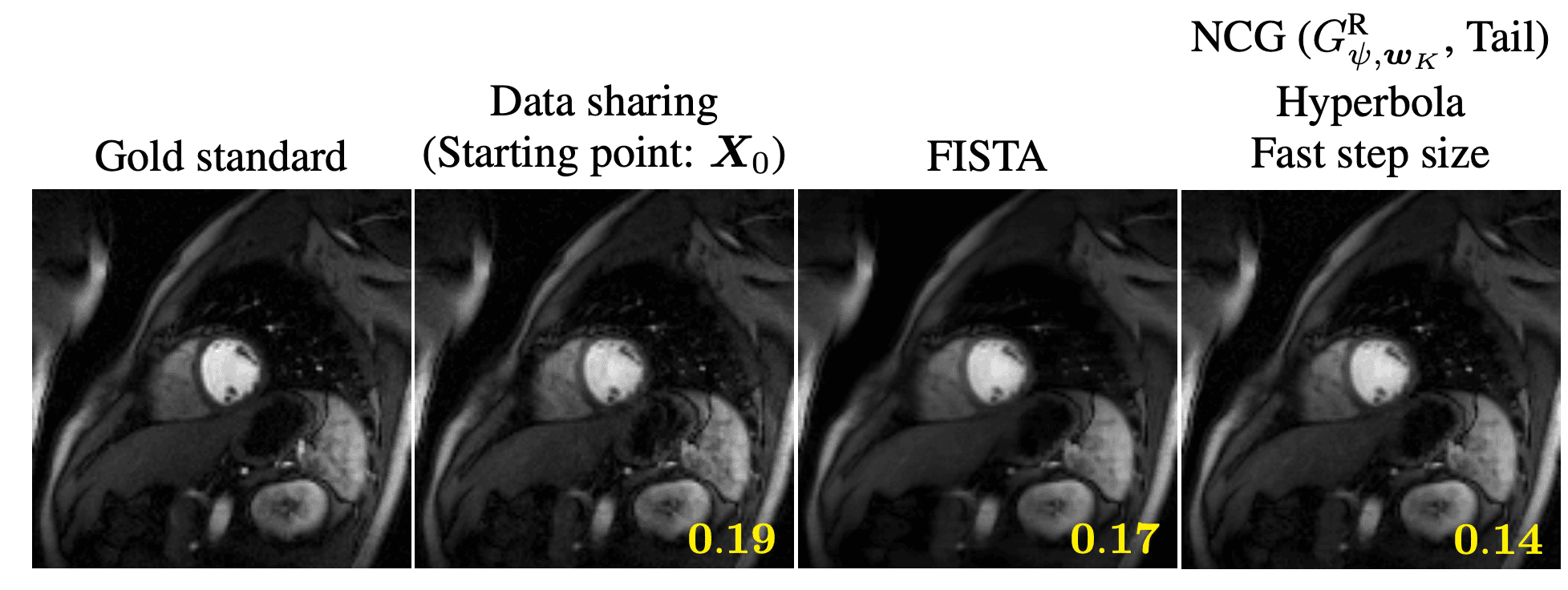
Many inverse problems and signal processing problems involve low-rank regularizers based on the nuclear norm. Commonly, proximal gradient methods (PGM) are adopted to solve this type of non-smooth problems as they can offer fast and guaranteed convergence. However, PGM methods cannot be simply applied in settings where low-rank models are imposed locally on overlapping patches; therefore, heuristic approaches have been proposed that lack convergence guarantees. In this work we propose to replace the nuclear norm with a smooth approximation in which a Huber-type function is applied to each singular value. By providing a theoretical framework based on singular value function theory, we show that important properties can be established for the proposed regularizer, such as: convexity, differentiability, and Lipschitz continuity of the gradient. Moreover, we provide a closed-form expression for the regularizer gradient, enabling the use of standard iterative gradient-based optimization algorithms (e.g., nonlinear conjugate gradient) that can easily address the case of overlapping patches and have well-known convergence guarantees. In addition, we provide a novel step-size selection strategy based on a quadratic majorizer of the line-search function that leverages the Huber characteristics of the proposed regularizer. Finally, we assess the proposed optimization framework by providing empirical results in dynamic magnetic resonance imaging (MRI) reconstruction in the context of locally low-rank models with overlapping patches.