ALPCAH: Sample-wise Heteroscedastic PCA with Tail Singular Value Regularization

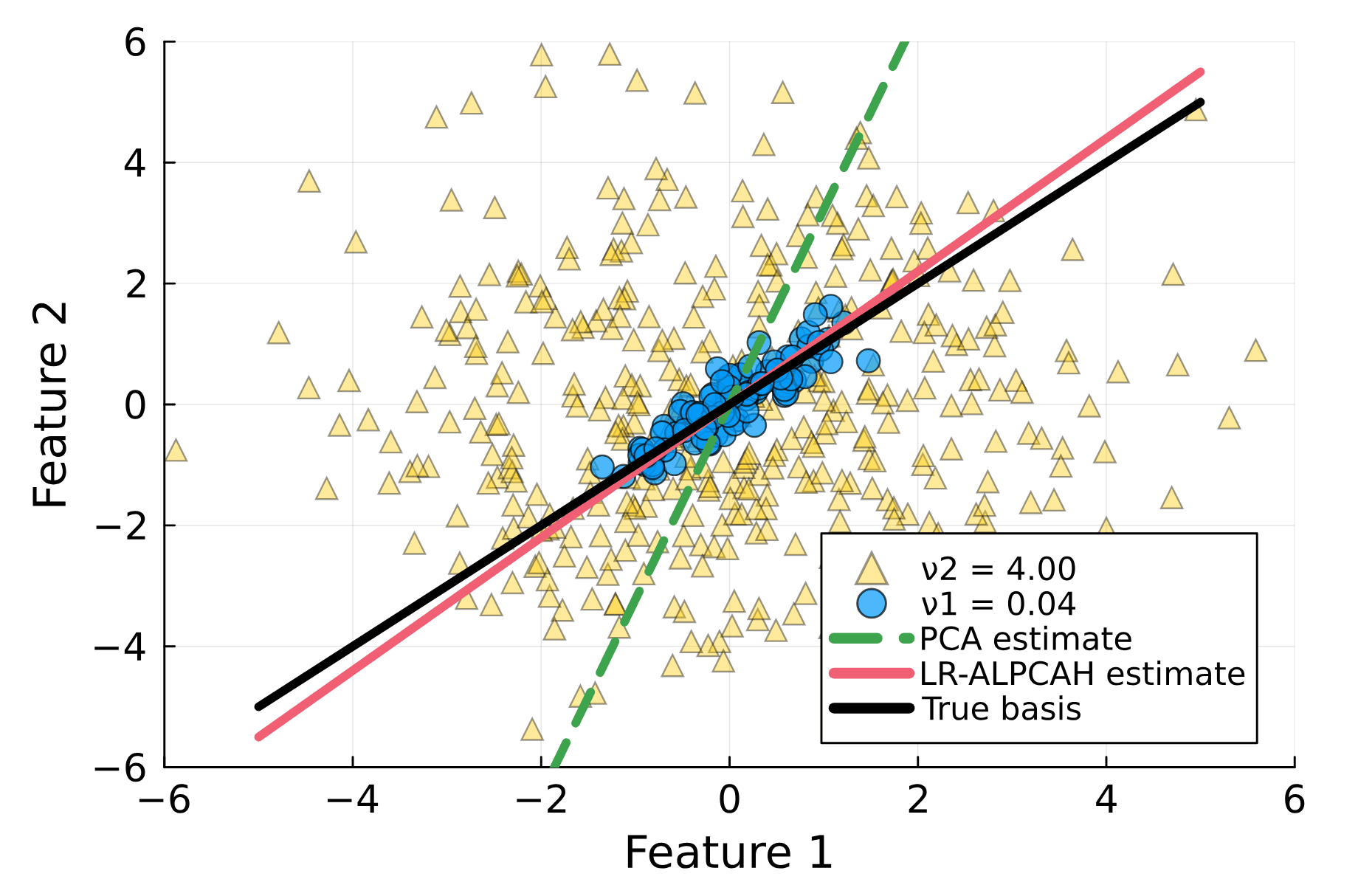
Principal component analysis (PCA) is a key tool in the field of data dimensionality reduction that is useful for various data science problems. However, many applications involve heterogeneous data that varies in quality due to noise characteristics associated with different sources of the data. Methods that deal with this mixed dataset are known as heteroscedastic methods. Current methods like HePPCAT make Gaussian assumptions of the basis coefficients that may not hold in practice. Other methods such as Weighted PCA (WPCA) assume the noise variances are known, which may be difficult to know in practice. This paper develops a PCA method that can estimate the sample-wise noise variances and use this information in the model to improve the estimate of the subspace basis associated with the low-rank structure of the data. This is done without distributional assumptions of the low-rank component and without assuming the noise variances are known. Simulations show the effectiveness of accounting for such heteroscedasticity in the data, the benefits of using such a method with all of the data versus retaining only good data, and comparisons are made against other PCA methods established in the literature like PCA, Robust PCA (RPCA), and HePPCAT. Code available at https://github.com/javiersc1/ALPCAH

Download paper here